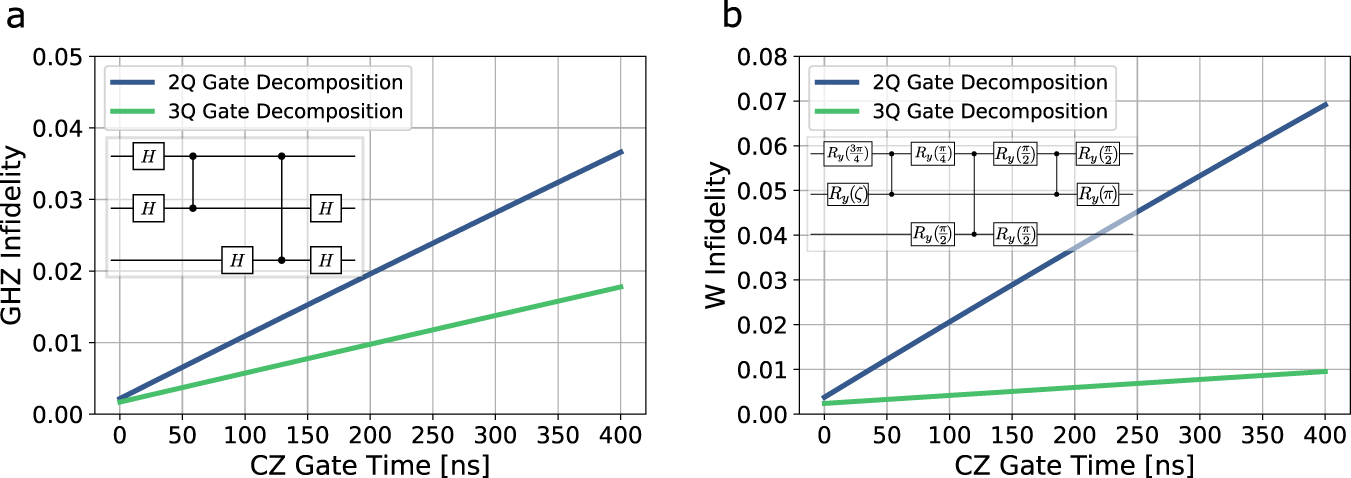
Comparison of coherence limits of GHZ state via compilation to two- or three-qubit gates.¶

In this tutorial we are going to recreate the results from the paper https://www.nature.com/articles/s41534-023-00711-x

Import Packages

In [1]:

import numpy as np
from qutip import tensor, basis, ket2dm, fidelity
from qutip_qip.circuit import QubitCircuit
from qutip_qip.operations.gates import rz
from chalmers_qubit.devices.sarimner import (
    SarimnerProcessor,
    SarimnerModel,
    SarimnerCompiler,
    DecoherenceNoise,
)
from chalmers_qubit.utils.operations import project_on_qubit

import warnings
warnings.simplefilter(action="ignore", category=FutureWarning)

import numpy as np from qutip import tensor, basis, ket2dm, fidelity from qutip_qip.circuit import QubitCircuit from qutip_qip.operations.gates import rz from chalmers_qubit.devices.sarimner import ( SarimnerProcessor, SarimnerModel, SarimnerCompiler, DecoherenceNoise, ) from chalmers_qubit.utils.operations import project_on_qubit import warnings warnings.simplefilter(action="ignore", category=FutureWarning)

Create GHZ-circuit for 3 qubits: One circuit is uing th three-qubit gate, the other one is using a two-qubit gate.

In [2]:

from chalmers_qubit.utils.gates import cczs

def ghz_two_qubit_gate():
    # Circuit to create GHZ-state using 2-qubit gate
    circuit = QubitCircuit(3)
    circuit.add_gate("H", targets=0)
    for i in range(1, 3):
        circuit.add_gate("H", targets=i)
        circuit.add_gate("CZ", controls=0, targets=i)
        circuit.add_gate("H", targets=i)
    return circuit

def ghz_three_qubit_gate():
    # Circuit to create GHZ-state using 3-qubit gate
    circuit = QubitCircuit(3)
    circuit.user_gates = {"CCZS": cczs}
    circuit.add_gate("H", targets=0)
    for i in range(1, 2):
        circuit.add_gate("X", targets=i)
        circuit.add_gate("CCZS", targets=[0, i, i + 1], arg_value=[np.pi / 2, 0, 0])
        circuit.add_gate("X", targets=i)
    return circuit

from chalmers_qubit.utils.gates import cczs def ghz_two_qubit_gate(): # Circuit to create GHZ-state using 2-qubit gate circuit = QubitCircuit(3) circuit.add_gate("H", targets=0) for i in range(1, 3): circuit.add_gate("H", targets=i) circuit.add_gate("CZ", controls=0, targets=i) circuit.add_gate("H", targets=i) return circuit def ghz_three_qubit_gate(): # Circuit to create GHZ-state using 3-qubit gate circuit = QubitCircuit(3) circuit.user_gates = {"CCZS": cczs} circuit.add_gate("H", targets=0) for i in range(1, 2): circuit.add_gate("X", targets=i) circuit.add_gate("CCZS", targets=[0, i, i + 1], arg_value=[np.pi / 2, 0, 0]) circuit.add_gate("X", targets=i) return circuit

We can plot the circuits

In [3]:

ghz_two_qubit_gate()

ghz_two_qubit_gate()

Out[3]:

In [4]:

ghz_three_qubit_gate()

ghz_three_qubit_gate()

Out[4]:

Define three-qubit device parameters

In [5]:

transmon_dict = {
    0: {"frequency": 5.02, "anharmonicity": -0.3},
    1: {"frequency": 5.47, "anharmonicity": -0.28},
    2: {"frequency": 5.25, "anharmonicity": -0.34},
}
decoherence_dict = {
    0: {"t1": 60e3, "t2": 100e3},
    1: {"t1": 80e3, "t2": 105e3},
    2: {"t1": 70e3, "t2": 103e3},
}
# Compiler options
options = {
    "dt": 0.01, # time step in (ns)
    "two_qubit_gate": {
        "buffer_time": 0,
        "rise_fall_time": 0,
    },
}

transmon_dict = { 0: {"frequency": 5.02, "anharmonicity": -0.3}, 1: {"frequency": 5.47, "anharmonicity": -0.28}, 2: {"frequency": 5.25, "anharmonicity": -0.34}, } decoherence_dict = { 0: {"t1": 60e3, "t2": 100e3}, 1: {"t1": 80e3, "t2": 105e3}, 2: {"t1": 70e3, "t2": 103e3}, } # Compiler options options = { "dt": 0.01, # time step in (ns) "two_qubit_gate": { "buffer_time": 0, "rise_fall_time": 0, }, }

Write a script to loop over different cz-gate times

In [6]:

def run_sarimner_simulation(circuit, transmon_dict, decoherence_dict, options_dict=None):
    # Simulation parameters
    tlist = np.linspace(20, 200, 10)  # Times in (ns)
    fidelities = []

    for t in tlist:
        # Calculate the corresponding coupling strength
        g = 1 / (np.sqrt(2) * 2 * t)
        coupling_dict = {(0, 1): g, (0, 2): -g}

        # Set up the model, compiler, and processor
        model = SarimnerModel(transmon_dict=transmon_dict, coupling_dict=coupling_dict)
        compiler = SarimnerCompiler(model=model, options=options)
        noise = [DecoherenceNoise(decoherence_dict=decoherence_dict)]
        sarimner = SarimnerProcessor(model=model, compiler=compiler, noise=noise)

        # Load circuit
        sarimner.load_circuit(circuit)

        # Simulate circuit
        init_state = tensor([basis(3, 0)] * 3)
        res = sarimner.run_state(
            init_state=init_state, options={"nsteps": 1e6, "atol": 1e-12}
        )

        # Post-process results
        final_state = project_on_qubit(res.states[-1])
        qubit_state = rz(np.pi, N=3) * final_state * rz(np.pi, N=3).dag()

        # Calculate fidelity
        ideal_state = circuit.compute_unitary() * tensor([basis(2, 0)] * 3)
        fidelities.append(fidelity(qubit_state, ideal_state))

    return tlist, fidelities

def run_sarimner_simulation(circuit, transmon_dict, decoherence_dict, options_dict=None): # Simulation parameters tlist = np.linspace(20, 200, 10) # Times in (ns) fidelities = [] for t in tlist: # Calculate the corresponding coupling strength g = 1 / (np.sqrt(2) * 2 * t) coupling_dict = {(0, 1): g, (0, 2): -g} # Set up the model, compiler, and processor model = SarimnerModel(transmon_dict=transmon_dict, coupling_dict=coupling_dict) compiler = SarimnerCompiler(model=model, options=options) noise = [DecoherenceNoise(decoherence_dict=decoherence_dict)] sarimner = SarimnerProcessor(model=model, compiler=compiler, noise=noise) # Load circuit sarimner.load_circuit(circuit) # Simulate circuit init_state = tensor([basis(3, 0)] * 3) res = sarimner.run_state( init_state=init_state, options={"nsteps": 1e6, "atol": 1e-12} ) # Post-process results final_state = project_on_qubit(res.states[-1]) qubit_state = rz(np.pi, N=3) * final_state * rz(np.pi, N=3).dag() # Calculate fidelity ideal_state = circuit.compute_unitary() * tensor([basis(2, 0)] * 3) fidelities.append(fidelity(qubit_state, ideal_state)) return tlist, fidelities

In [7]:

tlist, fidelities_2 = run_sarimner_simulation(ghz_two_qubit_gate(), transmon_dict, decoherence_dict, options)

tlist, fidelities_2 = run_sarimner_simulation(ghz_two_qubit_gate(), transmon_dict, decoherence_dict, options)

In [8]:

tlist, fidelities_3 = run_sarimner_simulation(ghz_three_qubit_gate(), transmon_dict, decoherence_dict, options)

tlist, fidelities_3 = run_sarimner_simulation(ghz_three_qubit_gate(), transmon_dict, decoherence_dict, options)

In [9]:

import matplotlib.pyplot as plt

plt.plot(tlist, (1 - np.array(fidelities_2)) * 100, "-x", label="cz")
plt.plot(tlist, (1 - np.array(fidelities_3)) * 100, "-x", label="cczs")
plt.legend()
plt.ylabel("Infidelity %")
plt.xlabel("CZ-gate time (ns)")
plt.title("GHZ state")

import matplotlib.pyplot as plt plt.plot(tlist, (1 - np.array(fidelities_2)) * 100, "-x", label="cz") plt.plot(tlist, (1 - np.array(fidelities_3)) * 100, "-x", label="cczs") plt.legend() plt.ylabel("Infidelity %") plt.xlabel("CZ-gate time (ns)") plt.title("GHZ state")

Out[9]:

Text(0.5, 1.0, 'GHZ state')

If we compare this plot to Figure 5a. from the paper we see the same trend